
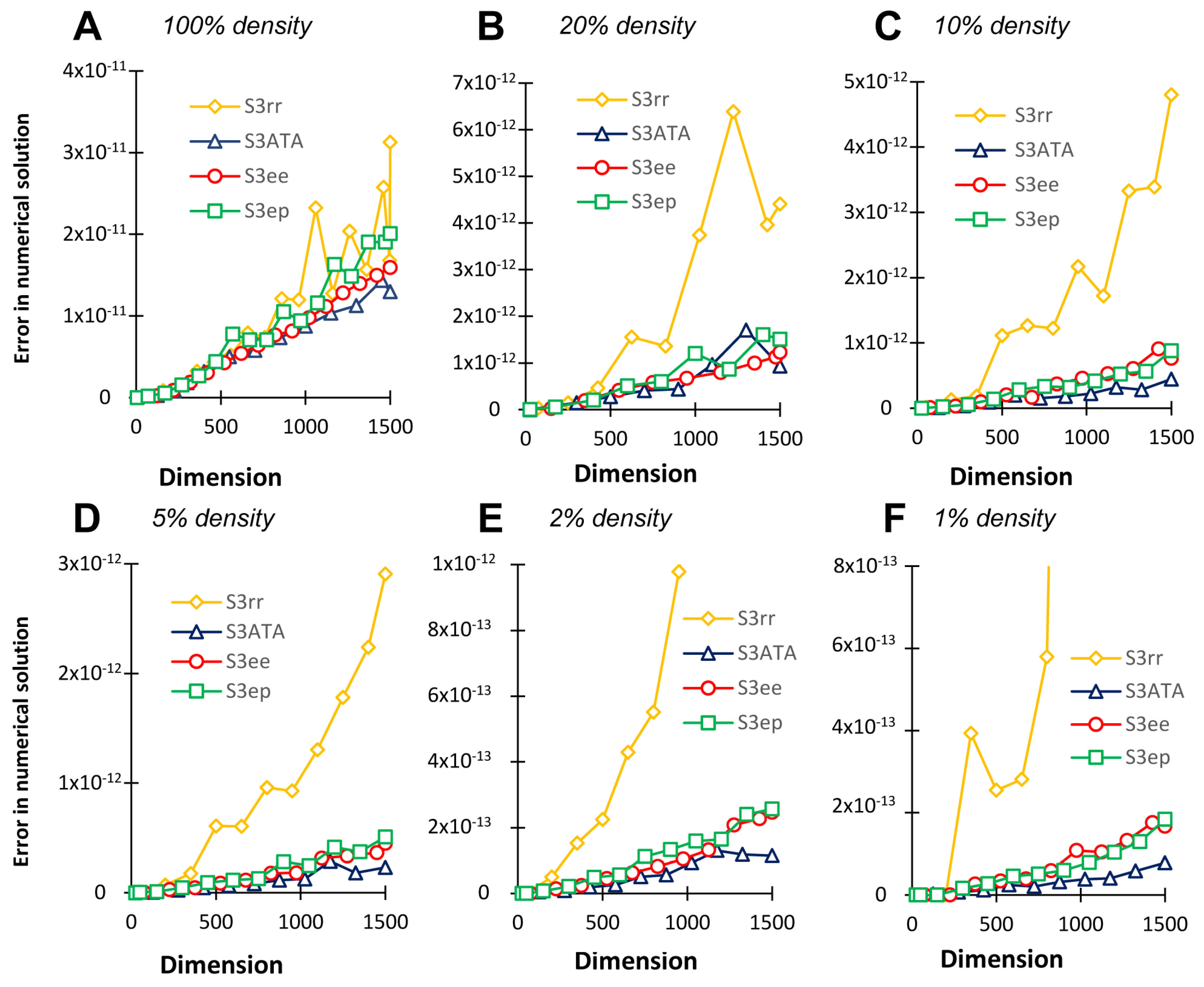
X and y where each is polynomial of order 2 or lessĪs would be true for equations describing geometrical """Return numerical solutions for 2 equations in The following is an example (with the potential for lots of numerical issues in corner cases): def n2solve(eq1, eq2, x, y, n): You would have to find roots one by one: > list(nsolve((eq1, eq2), (k,b), (1, 1)))īut one can use the existing tools to build a solver for such equations. There is no dedicated method (that I am aware of) that will compute all roots of a polynomial - in this case, a pair of quadratics - in SymPy/mpmath. There is, however, the function nsolve that can be used to find numerical solutions. SymPy intends to be a symbolic package, not numeric, so the results should be expected. That's what I got under MATLAB with 'solve'. That is not acceptable for my whole project. That's what I got under Python and Sympy, with an extremely small imaginary part.
Imaginary system of equations solver code#
But I think there must be something wrong in my code which result in slowly and imaginary part. I know that small imaginary part can be ignored. I also try the same computation under Matlab, the result is pretty good and fast.

The result is almost right, but always with a extremly small imaginary part, and the process is time consuming. , which systematically deals with linear systems of any size.I am trying to solve a system of nonlinear equations with Sympy and Python. The good thing about Cramer's method is that it works fine for small or larger systems, the approach is the sameįor larger systems of equations, the best alternative is to use the The approach used by this calculator is the use of This works fairly well on 2x2 systems of equations, but it can get cumbersome for larger systems Solving System of Equations by substitutionĪnother way of solving systems of equations is to write one variable in terms of the others and replace in the other equations. And the lines overlap (so they are the same line), then we have infinite solutions. Then, if the lines are parallel, we conclude that there are no solutions. The resulting graphs will be two lines.īy looking at the graph, we see that if the lines intersect, then there is a unique solution.
The way to go is to graph each equation as a function of one of the variables (typically, the variables are \(x\) and \(y\), and customarily \(y\) is used as the dependent variable). This approach only works for systems with two equations and two variables.

Indeed, based on the coefficients in the system, we are able to tell whether the system has a unique solution, or whether the system has many (infinite) solutions, or whether the system does not have solutions. The good thing about a system of equations is that there are some standard ways of solving them. Most systems will com defined with specific numbers whereas others come with literal constants, and are called There are many types of systems, with different characteristics and specific features. Either when you are solving a simple word problem or a complex allocation system, you are likely to end up solving a system of equations. Solving systems of equation is a common task in Algebra, because of its multiple applications.


 0 kommentar(er)
0 kommentar(er)
